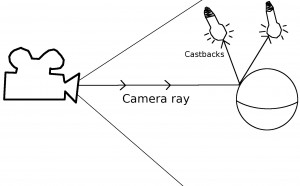
data Ray_Path = Ray_Path {hit :: Intersection, ref :: Ray_Path, thru :: Ray_Path, light_hits :: [Light_Castback]} |
Now we have the data in the Ray Paths, we need to write some shaders that use them:
shader_lit_red_ref :: Shader shader_lit_red_ref depth rp | depth > 10 = (0,0,0) | otherwise = blend [0.7, 0.3] [(shader_lit_red depth rp), (shade (depth + 1) (ref rp))] |
What this does is blend (a weighted average) the color we would get if we just did a simple diffuse shading with a red color and the color we get from the reflection. Notice that we’ve needed to add a counter for the depth to occur the infinite recursion you’d get if you held 2 mirrors up facing each other. This shader is the same idea but blends both the reflected and the through ray:
glass :: Shader glass depth rp | depth > 10 = (0,0,0) | otherwise = blend [0.2, 0.4, 0.4] [(shader_lit_grey depth rp), (shade (depth + 1)(ref rp)), (shade (depth + 1) (thru rp))] |
And here’s an image of a reflective red plane with a glass sphere (which really doesn’t look much like glass) on it: